Числовая система
Математики эпохи эллинизма пользовались неск. Ч. с., важнейшими из которых были аттическая (или Геродианова), милетская, рим. и шестидесятиричная Ч. с., заимствованная из Месопотамии. В основе Ч. с. лежат пальцевой счёт и счёт на абаке. Нужды торговли вызвали появление письм. Ч. с. уже в ионийский период греч. математики. Рим. Ч. с. – древнеиталийского происхождения. Аттич., или Геродианова, Ч. с. служила торговым целям – фиксации денежных сумм, кол-ва товара и обозначению отделений абака. Она представляла собой десятеричную систему с прибавлением чисел, кратных пяти. Единицы обозначались чертами (1). Степени десяти были обозначены начальными буквами соответствующих греч. числительных, т. е.
: Δ = 10 (deka – десять),
Н = 100 (hekaton – сто),
X = 1000 (chilioi – тысяча),
М = 10000 (myrioi – десять тысяч).
Сочетание с этими четырьмя знаками буквы П (от pente – пять), выглядевшей в архаич. графике как Г, увеличивало число в пять раз, напр., ГΔ = 50, ГХ = 5000. Милетская Ч. с. лучше, чем аттич., была приспособлена для письм. счета и поэтому использовалась в научном обиходе, в частности Архимедом и Диофантом. Буквы алфавита (первоначально 27) получали числовое значение:
1, 2, .., 9
10, 20, .., 90
100, 200, .., 900.
Т. к. 24 букв греч. алфавита (с 403 до н. э.) не хватало, то числовые значения были приписаны к трём семитским буквам: Ƒ (фау), G (коппа) и Ϡ (сампи). Т. о., Ч. с. приобрела следующий вид:
| единицы | А | Β | Γ | Δ | Е | Ƒ | Ζ | Η | Θ |
| α | β | γ | δ | ε | ϛ | ζ | η | ϑ | |
| десятки | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Q |
| ι | κ | λ | μ | ν | ξ | ο | q | ||
| сотни | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | Ϡ |
| ρ | σ | τ | υ | φ | χ | ψ | ω | ϡ | |
| тысячи | ˏα | ˏβ | ˏγ | ˏδ | ˏε | ˏϛ | ˏζ | ˏη | ˏϑ |
Числовая система. Милетская числовая система
Кол-во десятков тысяч (мириад) обозначалось надписыванием множителя над буквой М, имевшей значение «10.000» (от греч. myrioi), напр.
| λβ | |
| Μ | = 32 * 10.000 = 320.000 |
Позднее был изобретён иной способ: над буквами множителя надписывали по две точки, напр.:
| λβ | = 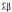 |
| Μ |
Более высокие степени, необходимость в обозначении которых возникала, напр., у Архимеда в его «Исчислении песчинок», обозначались каждым автором по-разному. Употребление букв в числовом значении могло привести к ошибкам, во избежание которых цифры выделялись либо чёрточкой справа сверху, либо горизонтальной полосой сверху: αρμε´ = ̅α̅ρ̅μ̅ε= 1.145. Рим. Ч. с. была десятиричной и содержала знаки I, X, С (100), CIC (1.000, позднее писался как М, от mille – тысяча). Путём деления последних трёх знаков пополам были образованы знаки для 5 (V), 50 (L) и 500 (D). Характерная особенность рим. Ч. с. – использование не только принципа сложения, но и принципа вычитания (напр., 19 = 20–1). Этот способ записи, несмотря на громоздкость, просуществовал вплоть до средних веков. Неприспособленность описанных Ч. с. для операций с большими числами заставила астрономов эллинистич. периода заимствовать из Вавилонии позиционную систему с основанием 60 – шестидесятиричную Ч. с. Совр. Ч. с., также позиционная, имеет основанием число 10 и называется десятеричной. К примеру, дробь 1¼ соответствует десятичной дроби 1,25 = 1 + 2/10 + 5/100 и шестидесятиричной дроби
1,15 = 1 +15/60. Уже Гиппархом Никейским (ок. 190 – после 126 до н. э.) в шестидесятиричной Ч. с. была рассчитана таблица длин хорд круга, а начиная с Птолемея эта система становится в астрономии общеупотребительной. К ней восходит деление окружности на 360 градусов, углового градуса – на 60 минут, минуты – на 60 секунд и т. д.
